EJERCICIOS MOVIMIENTO ONDULATORIO
Problema 1. La velocidad de
propagación de una onda es de 330 m·s-1 y
su frecuencia 103 Hz. Calcular:
a ) la diferencia de fase dos posiciones de una misma
partícula que se presentan en intervalos de tiempo separados
b ) la diferencia de fase en un determinado instante
entre dos partículas que distan entre sí
c ) la distancia que existe entre dos partículas que se encuentran desfasadas
120º.
Problema 2. Determinar la ecuación de una onda armónica que se propaga en el
sentido negativo del eje OX con una velocidad de 900 ms-1,
siendo su frecuencia de 400 Hz. y su amplitud de 0'
Problema 3. Un foco puntual realiza un movimiento periódico representado por la
ecuación
Se pide determinar:
a ) velocidad de la onda.
b ) Diferencia de fase para dos posiciones de la misma
partícula cuando el intervalo de tiempo transcurrido es de 1 segundo.
c ) Diferencia de fase en un instante dado de dos
partículas separadas
d ) Si el desplazamiento y(x,t) de una determinada
partícula en un instante determinado es de
Problema 4. Calcular la energía que posee una molécula de agua cuando a ella
llega una onda de 103 Hz. y vibra con una
amplitud de 0'
Datos: masa molecular del agua: 18'085 gr., nº de Avogadro: 6,023x1023.
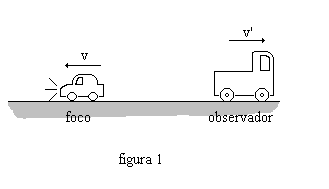
Problema 5. Un automóvil se mueve hacia la izquierda con una velocidad v = 30 m·s-1. En dirección contraria (rebasado
suficientemente el punto de cruce) va un camión a una velocidad v' = 21 m·s-1, con una gran superficie reflectora en la
parte posterior (figura 1). El automóvil
emite un bocinazo (emisión instantánea) con una frecuencia de 1000 Hz.
Determinar:
a ) la frecuencia de las ondas percibidas por el observador
situado a la derecha del coche.
b ) la frecuencia de las ondas que llegan a la
superficie reflectora del camión.
c ) la frecuencia de las ondas que percibirá el
observador después de que las ondas se hayan reflejado en el camión.
d ) la frecuencia de las ondas que percibirá el
conductor del coche después de la reflexión en el camión.
Dato: velocidad del sonido: 330 ms-1, se
supone el aire en calma.
Problema 6. Dos ondas que se mueven en la misma dirección y cuyas ecuaciones
escritas en el sistema CGS son
Determinar:
a ) la ecuación de la onda resultante
b ) la amplitud de los vientres
c ) la distancia entre dos nodos consecutivos
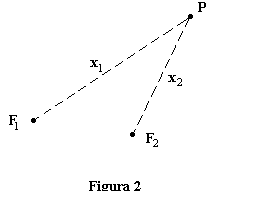
Problema 7. Dos focos sonoros emiten simultáneamente ondas de la misma
frecuencia n = 425 Hz.
y la misma amplitud, siendo la velocidad del sonido en el aire c = 340 m·s-1. Si colocamos un aparato registrador de
sonidos a x1 =
Problema 8. La ecuación de una onda estacionaria particular sobre una cuerda es :
y = 0'15·(sen 5·x cos 300·t) m.
Encontrar:
a ) amplitud de la vibración en el vientre
b ) distancia entre nodos
c ) longitud de onda
d ) frecuencia
e ) velocidad de la onda
Problema 9. El coeficiente de absorción en un determinado medio es 0'5 m-1.
a ) ¿Cuál ha de ser su espesor para que la amplitud de
la onda plana que lo atraviesa disminuya a la mitad de la incidente?
b ) ¿en qué factor se reducirá la intensidad incidente
al atravesar dicho espesor?
Problema 10. Un movimiento ondulatorio unidimensional armónico viene descrito
por la ecuación:
y(x,t) = 0'002·sen (60·x + 300·t)
donde y indica el desplazamiento de las partículas del medio respecto de su posición de equilibrio (x en metros y t en segundos). Determine:
a ) el sentido en el que se propaga la onda y su
velocidad
b ) la longitud de onda y frecuencia del movimiento
c ) la energía cinética con al que oscila un punto material del medio de masa m
= 0'5 gr. situado en x = 2'
d ) la distancia entre las posiciones de dos puntos
cuya diferencia de fase es de p/2
e ) la frecuencia medida por un observador que se mueve en la misma dirección
con una velocidad de 500 m·s-1 acercándose
hacia la fuente, supuesta inmóvil (csonido
= 330 m·s-1).
Problema 11. La ecuación de cierta onda armónica es :
y(x,t) = 3·cos 2p(16·t - 2·x)
donde x y y se expresan en metros y t en segundos.
Determinar:
a ) la amplitud, longitud de onda, frecuencia,
frecuencia angular y velocidad de propagación de la onda
b ) la velocidad y aceleración máximas de un punto del medio
c ) ecuación de la onda que al combinarla con la anterior produzca ondas
estacionarias
d ) ecuación de la onda estacionaria, indicando cuál será su amplitud,
distancia entre dos nodos y distancia entre un nodo y un vientre